Cálculo da força de flexão durante a flexão livre da máquina de dobrar chapas metálicas

Nos últimos anos, as dobradeiras com freios metálicos têm sido amplamente utilizadas em várias indústrias, e a gama de processamento das máquinas dobradeiras vem se expandindo. No entanto, não tem havido uma discussão sistemática sobre o cálculo da força de flexão. Atualmente, existem aproximadamente dois tipos de fórmulas de cálculo de força de flexão recomendadas nos manuais de vários fabricantes de dobradeiras de dobradeiras.

P - força de flexão, KN;

S - espessura da chapa, mm;

l - o comprimento de flexão da chapa, m;

V - a largura da abertura inferior da matriz, mm;

σb - Resistência à tração do material, MPa.

A tabela de parâmetros de força de flexão recomendada pelo fabricante também é calculada de acordo com a fórmula acima.

O processo de derivação e o escopo de aplicação da fórmula de cálculo da força de flexão

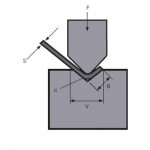
A Figura 1 é um diagrama esquemático do trabalho durante a dobra da chapa. O seguinte descreve o processo de derivação da fórmula de cálculo da força de flexão e duas condições de parâmetros adicionais. Primeiro, existem essas recomendações no manual do produto. Na dobra livre, a largura de abertura da matriz inferior selecionada V é de 8 a 10 vezes a espessura da chapa S. Aqui tomamos a relação de aspecto .

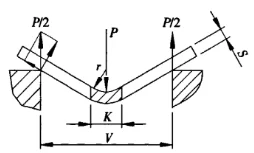
Figura 1 Diagrama esquemático de flexão

P - força de flexão

S - espessura da folha

V - largura de abertura da matriz inferior

r - o raio interno quando a folha é dobrada

K - a largura da projeção horizontal da zona de deformação de flexão=9

Em segundo lugar, o fabricante lista os valores correspondentes da largura da matriz V e do diâmetro interno r da peça de trabalho de dobra na tabela de parâmetros de força de dobra. Geralmente r=(0,16~0,17)V. Aqui, a relação diâmetro-largura =0.16.

Durante o processo de dobra da chapa metálica, o material na zona de deformação está em um estado de deformação altamente plástica e é dobrado em um ângulo em torno da linha central. Na superfície externa da zona de flexão, microfissuras podem aparecer em alguns casos. Na seção transversal da zona de deformação, exceto na vizinhança da camada central, as tensões em outros pontos estão próximas da resistência à tração do material. A parte superior da camada neutra é comprimida e a parte inferior é tensionada. A Figura 2 mostra uma seção transversal e diagrama de tensão correspondente na zona de deformação.

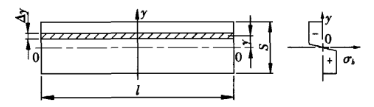
Figura 2 Diagrama de tensão

S - espessura da folha

l - comprimento de dobra da folha

O momento fletor na seção transversal da zona de deformação é:

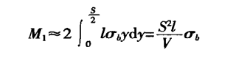
O momento de flexão gerado pela força de flexão da máquina na zona de deformação é (ver Figura 1):

A partir de

Ao usar moldes de uso geral para dobra livre em uma máquina de dobra, a maior parte da chapa metálica é dobrada em 90°. Conforme mostrado na Figura 3. K é:

Substituindo K na equação (1), temos:

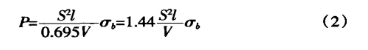
A resistência à tração de materiais comuns σb=450N/mm2, substituindo a fórmula (2) por:

Pode ser visto a partir do processo de derivação que ao usar a equação (2) ou equação (3) para calcular a força de flexão, as duas

as condições dos parâmetros mencionadas acima precisam ser atendidas. Ou seja, a proporção= 9, a razão diâmetro-largura=0,16, caso contrário causará um grande erro.

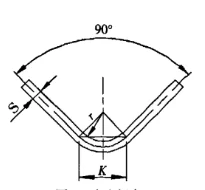
Figura 3 Flexão livre

S - espessura da folha

r - o raio interno quando a folha é dobrada

K - a largura da projeção horizontal da zona de deformação de flexão

Novos métodos e etapas para calcular a força de flexão

Devido a requisitos de projeto ou processo, às vezes é difícil atender aos dois requisitos adicionais acima ao mesmo tempo. Neste momento, a fórmula de cálculo recomendada não deve ser usada para calcular a força de flexão, mas deve ser realizada de acordo com as etapas a seguir.

(1) De acordo com a espessura da placa S, o raio de curvatura r, e a abertura inferior da matriz V, a relação largura/espessura e a relação diâmetro/largura são calculadas respectivamente.

(2) Calcule a largura de projeção da zona de deformação de acordo com a deformação da chapa.

(3) Aplique a fórmula (1) para calcular a força de flexão.

No processo de cálculo foi considerada a diferença do raio de curvatura e a mudança da zona de deformação correspondente. A força de flexão calculada a partir disso é mais precisa e confiável do que o resultado calculado pela fórmula normalmente recomendada. Agora dê um exemplo para ilustrar, como mostrado na Figura 4.

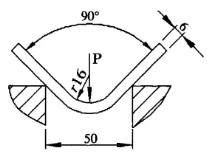
Figura 4 Novo método de cálculo

Conhecido: A espessura da folha S=6mm, o comprimento da folha l=4m, o raio de curvatura r=16mm, a largura da abertura da matriz inferior V=50mm, e a resistência à tração do material σb=450N/mm2. Encontre a força de flexão necessária para flexão livre.

Primeiro, encontre a proporção e a proporção diâmetro/largura:

Em segundo lugar, calcule a largura de projeção da zona de deformação:

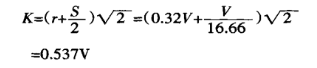
Finalmente, use a equação (1) para encontrar a força de flexão:

Se a fórmula usual recomendada for usada para calcular a força de flexão:

A partir de = 1,5, pode-se ver que a diferença entre os dois é de 1,5 vezes. A razão para este erro é que o raio de curvatura neste exemplo é relativamente grande e a área de deformação correspondente é aumentada, de modo que uma força de curvatura maior é necessária durante a curvatura. Neste exemplo, a razão diâmetro/largura=0,32, que excedeu as condições adicionais dos parâmetros introduzidos acima. Obviamente, é inapropriado usar a fórmula normalmente recomendada para calcular a força de flexão. Você pode ver as vantagens do novo método de cálculo neste exemplo.

Conclusão

As etapas e fórmulas para calcular a força de flexão aqui introduzidas não são apenas aplicáveis à flexão angular de chapas metálicas, mas também à flexão a arco (estritamente falando, deve ser chamada de flexão angular com um raio de curvatura extragrande). Deve-se ressaltar que a forma do molde é especial quando a folha é dobrada em forma de arco. Ao calcular a projeção da zona de deformação, ela deve ser calculada de acordo com os parâmetros tecnológicos definidos no processo tecnológico, que não podem ser expressos por uma fórmula simples.

Ao projetar um molde em forma de arco, usando o método apresentado neste artigo para calcular a força de flexão, podem ser obtidos resultados satisfatórios.